Data structure
In computer programming, a data structure is a predefined format for efficiently storing, accessing, and processing data in a computer program. Some data structures are a programming language built-in component, and others may require the inclusion of a library or module before the structure can be used.
The decision of what data structures to use and how they're used is one of the most important steps in designing and writing a computer program.
"Bad programmers worry about the code. Good programmers worry about data structures and their relationships." — Linus Torvalds
Primitive data structures
The following are primitive data structures, also known as data types. Each of the following primitives can hold a single value, such as 1, 3.14, or the lowercase letter a.
| Name | Description | Example values |
|---|---|---|
| Boolean | A boolean data type can represent one of only two possible values: true or false, stored internally as "1" or "0." It is named after mathematician George Boole, whose system of logical operations is the foundation of all binary computers. | True, False, 1, 0 |
| Character | A character represents a single visual or alphanumeric symbol. Internally, it is represented as a number. Depending on the character encoding type, a character may be stored in a single byte (eight bits) or multiple bytes (for example, 16 bits for UTF-16 Unicode). When multiple characters are connected in sequence, such as the word "apple" or the sentence "I would like an apple," they form a string. | A, a, 5, ?, © |
| Integer | A whole number that falls within certain numerical limits. The limits are dependent on the programming language, and sometimes on the architecture of the CPU (central processing unit). Integers may be signed (positive or negative) or unsigned (restricted to positive values only). The maximum value of a 32-bit signed integer is 2147483647 (2 x 1031 - 1), and the minimum value is -2147483648 (-2 x 1031). | 1, 123, -2147483648 |
| Floating-point | A floating-point number can represent numbers with a fractional component — numbers with digits after a decimal point. The decimal point can "float," meaning it can appear at any position in the number. Internally, a float is similar to scientific notation (e.g., 1618033 x 10-6 = 1.618033), with a stored exponent (in this case, -6) representing the position of the decimal point. Floating-point numbers are signed — they can store either positive or negative values. | 1.567001, 0.356000, -5000.01 |
| Double-precision floating-point | A double-precision floating-point uses twice the number of bytes of a standard float, providing approximately double the precision. | 3.00000012384632, -351691.581045892 |
| Pointer, also called a reference, handle, or descriptor | A pointer is a special value that refers ("points") to a memory location where a data object (e.g., a data structure or a function) is stored. Pointers are a powerful feature of some low-level languages, but they are dangerous if implemented incorrectly, and may cause severe bugs or software vulnerabilities. Some languages do not support pointers. Other languages do, but require that the pointer be "typed" — the programmer must explicitly declare the type of data of where it points. Accessing a value by its pointer is called dereferencing. | 0xffe2ba6c, 0xffe2ac5b |
| Fixed-point | A numeric value with a whole number and fractional component, similar to a floating-point number, but with a preset level of precision. For example, monetary values can usually be represented in a fixed-point format that always has two digits after the decimal point, e.g., 5.00 or 123.45. Most programming languages do not natively support a fixed-point data type, because floating-point is more flexible. Languages with fixed-point data types include Ada and COBOL (Common Business Oriented Language). | 1.2, 400.00, -9.874 |
Compound data structures
Compound data structures can contain multiple elements. These elements are usually values of a primitive data type, such as an integer or character. Some compound structures are restricted to a single data type, while others permit a mixture of data types. Some can contain data structures as elements.
Each of the following compound structures has its own benefits and use cases.
Linear data structures
A linear data structure is a compound data structure whose elements are arranged in a logical sequence. In these structures, every element is followed by exactly one other element, unless it is the last one.
| Name | Description |
|---|---|
| Array | An array is a sequence of elements, usually of a single data type. Each element can be accessed by an index number representing its position in the array. Usually, array indexing is zero-based: if the array contains n elements, the first element has index 0, the second has index 1, and the last has index n-1. For example, consider an array named primes containing the values [2, 3, 5, 7, 11]. The first element, primes[0], is the value 2. The last element, primes[4], is the value 11. The length of this array (the number of elements it contains) is 5. A static array cannot change in size once it is declared and its memory allocated. A dynamic array can increase or decrease in length as needed. A LUT (lookup table) is an array containing pre-calculated values to speed up computation. For example, a LUT may contain frequently-used square roots of numbers. When the square root of a number is needed in a calculation, the value is "looked up" in the array, rather than computed, conserving CPU cycles. A multidimensional array contains fixed-length arrays as elements. For example, [[1, 2], [3, 4], [5, 6]] is a two-dimensional array. It contains three elements, each of which is an array. The values can be accessed by providing two index numbers, one for each array. In this example, the value at index [0][0] is 1. At index [0][1] is the value 2. At index [1][0] is the value 3. The last value, at index [2][1], is 6. A matrix is a mathematical object that can be implemented as a multidimensional array. |
| Associative array | An associative array, also called a dictionary, map, or symbol table, is a data structure containing pairs of keys and values. Every key must be unique (it should not appear more than once in the structure). Each key is associated with a value, which does not need to be unique — multiple keys may have identical values. High-level languages often have built-in data types for working with associative arrays, such as the dict class in Python. An associative array may be implemented as a standard single-dimensional or two-dimensional array, if the programmer devises the proper scheme to properly index and associate keys and values. It may also be implemented as a hash table, a binary search tree, etc. JSON (JavaScript Object Notation) is a widely-used data structure for associating keys and values, designed by Douglas Crockford for JavaScript applications. JSON is essentially an associative array where the values may also be associative arrays. |
| List | A list is a sequence of elements. In its simplest form, a list can be implemented as an array. However, the term "list" usually refers to a linked list with each element of the list (called a "node") containing pointers to one or more other list items. Unlike an array, in a linked list, sequential elements are not arranged sequentially in physical memory. In a singly-linked list, each element contains a pointer to the next element in the list. In a doubly-linked list, each element has two pointers: one pointer to the next element, and one pointer to the previous. In a multiply-linked list, more than two pointers may be included in a node. These pointers can each have a special purpose, defined by the programmer, for traversing elements in an arbitrary sequence. For example, a node may have one pointer for the next node by alphabetical order, another pointer for the next node by chronological order, etc. Although a multiply-linked list may be traversed linearly, its multiple linkage may permit nonlinear traversal of the data structure. In a circular linked list, the last node points to the first, allowing for infinite traversal of the list. In other words, the next node after the last is the first. In general, linked lists are more flexible than arrays. For example, inserting an array element may require all or part of the array be re-written in memory, beginning at the location of the insertion. In contrast, inserting a node in a linked list requires only a single node be created, and the pointers of adjacent nodes be updated with the new node's location. The tradeoff is that linked lists require more system resources. For example, linked lists require either manual or automatic GC (garbage collection), to "clean up" (make available) memory that is no longer in use after nodes are removed from the list. |
| Queue | A queue is a sequential collection where elements are added to the end of the queue, and removed from the beginning. It is a FIFO data structure ("first in, first out"). It is most efficiently implemented with a doubly-linked list. A queue can also be implemented as a singly-linked list or a dynamic array, if two additional pointers are maintained, pointing to the first and last elements. Adding an element to a queue is called queueing, and removing an element from a queue is called dequeueing. |
| Stack | A stack is a sequential collection of elements where only the last element (at the "top" of the stack) can be modified. A new element can be "pushed" onto the stack, in which case, it becomes the last element of the stack, and the stack's length increases by 1. The last element can be "popped" from the stack, where it's returned as a value and removed from the stack, decreasing the stack's length by 1. Sometimes, a "peek" operation is also provided, allowing the last element to be read without being removed. A stack is a LIFO ("last in, first out") data structure: the last element added is always the next element removed. A stack can usually be implemented as an array or a linked list, with a separate pointer to the top element of the stack. |
| String | A string contains a sequence of characters. In some languages, a string is an array of characters, terminated with a null character. For example, the word "hope" could be represented by the array ['h', 'o', 'p', 'e', '\0']. In other languages, such as Python, strings are implemented as a class, with associated methods for processing, accessing, and manipulating the string's characters. |
| Tuple | A tuple is a sequential list of elements. It is usually implemented as an immutable object that allows mixed data types. To identify its size, it may be called an "n-tuple," i.e., "three-tuple," "six-tuple," etc., where n is the number of elements it contains. |
Tree structures
A tree is a compound structure whose elements are arranged in a parent-child hierarchy, similar to branches on a tree. The elements are called nodes. A tree contains a single root node, which has no parents. Traversal usually occurs only in one direction, from the node to one of its children (called "descendents"). Then, traversal continues recursively, to one of the children of that node, until the desired node is reached. If a node has no children, it is called a leaf node.
If a tree is balanced, all of its branches are same "depth" — all leaf nodes are the same distance from the root node. If a tree is unbalanced, there's no restriction of how long a branch can be in relation to the others. Unbalanced trees are simpler to implement, but may be less efficient in worst-case scenarios.
| Name | Description |
|---|---|
| Abstract syntax tree | An AST (abstract syntax tree) structures the elements of a computer program in a tree hierarchy. The structure of the tree naturally represents some elements of the syntax of a computer language, such as lexical scope and conditional statements. An AST has many uses in computer science, such as automatically converting a program from one language to another. |
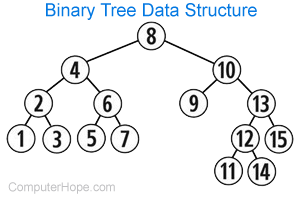
| Binary tree | In a binary tree, every node has zero, one, or two children. By some definitions, binary tree nodes must have exactly two children or none. An example of binary tree usage is a numerical comparison, where traversal of the tree is based on comparing two children and choosing the greater or lesser value. |
| B-tree | B-trees are tree structures where nodes may have more than two children, and are arranged according to their sorted values. B-trees are self-balancing, organized according to a given set of rules ensuring that fundamental operations occur in logarithmic time. In other words, the number of steps required to complete an operation, in the worst case, is never greater than the logarithm of the total number of tree elements. This property makes B-trees ideal for quick access of massive data storage, such as file systems and databases. |
| BSP tree | A BSP tree contains data used in binary space partitioning, where a geometric space is recursively, logically divided. BSP trees are frequently used in 3D graphics to optimize the rendering of objects in the space. For example, a space can be partitioned so objects partially obscured by other objects are not fully rendered, or not rendered at all, increasing performance. |
| Heap | A heap is a tree that satisfies the "heap property." In a max heap, for any node C, if P is a parent node of C, then the value (key) of P is greater than or equal to C. In a min heap, the value of P is less than or equal to the value of C. Heaps are commonly used as a priority queue, where the highest or lowest-priority item is stored at the root of the tree. Binary heaps (with a maximum of two nodes for any parent) are the fundamental data structure of the heap sort algorithm. |
| Merkle tree | A Merkle tree or hash tree is a tree structure with every parent node contains a cryptographic hash of its children, and leaf nodes contain a cryptographic hash of a block of data. They are useful for verifying the authenticity of data. For example, they are used in the IPFS (InterPlanetary File System), Btrfs, and ZFS (Zettabyte File System) file systems to verify that data has not been corrupted on disk. They are also used in the bitcoin and Ethereum cryptocurrency protocols to protect against malicious or incidental inconsistencies in the blockchain. Other systems that use Merkle trees include the Git and Mercurial version control systems, and the NoSQL database system Apache Cassandra. They are named after their inventor, Ralph Merkle. |
| R-tree | R-trees are tree structures optimized for certain spatial operations on the data. For example, they can store geographic locations, and efficiently find locations within a certain radius, based on the distance of their connecting roads. The "R" stands for rectangle, in reference to the fact that elements are grouped according to their minimum bounding rectangles within a geometric space. |
Hash structures
In computer science, a hash function is a function that produces a fixed-length number, often represented in hexadecimal, that can be calculated from a given set of input data. Regardless of the input size, as long as the input has not changed, it always produces the same fixed-length hexadecimal number. These types of functions have important uses in computer science, because they can validate or index data, even at a massive scale.
The following are examples of data structures designed to store the results of hash functions, many being special cases of structures described in the sections above.
| Name | Description |
|---|---|
| Bloom filter | A Bloom filter is a probabilistic data structure first proposed by scientist Burton Howard Bloom at MIT (Massachusetts Institute of Technology) in 1970. The mathematical properties of the structure allow a program to quickly determine if an element possibly or certainly does not belong to a larger set of elements. Bloom devised the structure to address problems in the growing fields of AI (artificial intelligence), ML (machine learning), and big data. Using traditional structures such as hash tables, deterministic queries on large sets of data would not be feasible, exceeding a practical amount of disk space and core memory. Using a Bloom filter, however, results can be obtained with a high degree of probability with a fraction of memory and disk access. The structure can be tuned according to available resources, providing massive efficiency gains for a negligible loss of accuracy. |
| Hash table | A hash table or hash map is a type of associative array where the keys are the computed hashes of their values. For example, the contents of files can be hashed to create a fixed-length key, e.g., a hexadecimal number with a constant number of digits. The algorithm assures that this key is almost certainly unique. Usually, there is a small probability of a "collision" in the table — different inputs have a small chance to produce identical keys. The chance of collision is usually negligible, and considered an acceptable tradeoff for high performance. Hash tables are a good way to index large data sets, providing search times that are independent of the table size. |
| Rolling hash | A rolling hash is a hash table whose hash function "rolls through" an input set, progressively computing hashes for a moving window of the input data. It is useful for processing data that is input in a steady stream, such as data transferred over a network. For example, rsync uses a rolling hash to protect against data corruption during network file transfers. The rolling hash is also useful in stream processing. In stream processing, computations are performed progressively on data sets too big to store all at once on a single device. |
| Trie | A trie (alternatively pronounced as "tree" or "try") is an ordered tree structure that stores associative arrays. It has special properties that make it space-efficient for certain search operations. In a trie, the key of a node is not stored literally. Instead, the key is defined by the node's position in the tree. The keys of all descendants of a given node share a common prefix, such as the first characters of a string, associated with the parent node. Tries are ideal for certain search functions, such as those used in NLP (natural language processing). The data structure was first described by computer scientist René de la Briandais in 1959, and the term "trie" was coined by Edward Fredkin in 1961. Fredkin derived the term from the word "retrieval," and pronounced it "tree." |
Graph structures
A graph is a data structure that organizes data according to the relationships of its elements in a geometric space. The elements are usually vertices (points in the graph) and edges (the connections between vertices).
If the vertices in a graph can be traversed in only one direction (A→B, but not B→A), it is called a directed graph. If vertices can be traversed in either direction, it is called an undirected graph. If it's possible to traverse edges and return at the starting vertex, it is called a cyclic graph. If such traversal is not possible, it is called an acyclic graph.
The following are examples of data structures used to efficiently store and process graphs.
| Name | Description |
|---|---|
| Adjacency list | An adjacency list is a collection of unordered lists, each of which describes the neighbors of a vertex in a graph. It may be implemented using other data structures, such as a hash table where the values are arrays of adjacent vertices. In other implementations, the vertices and edges are each stored as objects connected by pointers, similar to a multiply-linked list. An adjacency list can compute all neighbors of a vertex in constant time, proportional to the degree of the vertex (the dimensionality of the graph). However, it's inefficient for determining if an edge exists between two given vertices. |
| Adjacency matrix | In an adjacency matrix, a multidimensional array uses boolean values (requiring only one bit) corresponding to the connectedness of vertices, which are indexed to the matrix rows and columns. In this structure, listing the neighbors of a vertex takes longer to compute, proportional to the total number of vertices. In addition, the structure requires more storage, growing exponentially with the total number of vertices. However, determining if an edge exists between two vertices is significantly faster than with an adjacency list. |
| Graph-structured stack | A graph-structured stack is a data structure whose operations correlate to a traditional stack (a LIFO whose values can be pushed or popped), but the item connectedness of an acyclic graph. It has important uses in NLP (natural-language processing), specifically parsing ambiguous or non-deterministic grammars, such as those used by humans. |
| Hypergraph | In a hypergraph, an edge can join any number of vertices. These special edges, called hyperedges, usually share cardinality (they are all connected to the same number of nodes). In a k-uniform hypergraph, all hyperedges are connected to k nodes. For example, a "2-uniform hypergraph" is the same as a traditional graph; in a 6-uniform hypergraph, each hyperedge connects to 6 nodes. Hypergraphs have a special definition of acyclicity, with special rules for what constitutes traversal of nodes in a cycle. The mathematical properties of hypergraphs have gained attention with the advent of ML (machine learning), in applications such as recommendation systems and semi-supervised learning. |
| Scene graph | A scene graph is a structure used in some vector graphics editors, 3D modeling software, and computer games. It can efficiently model a complex relationship of objects that are spatially related, representing a hierarchy of sequential modifications. For example, when multiple geometry effects are applied to a 3D modeling object, each sequential modification is based on the results of the previous changes. A sphere may be created as a NURBS (Non-Uniform Rational Basis Spline) object, modified by a bounding lattice, then converted to wireframe geometry so its individual vertices can be transformed. These modifications could be stored in a scene graph, so the final result of all transformations can be efficiently animated or rendered as single objects. Modifying any single step in the modification chain would not destroy the transformations occurring later in the sequence. |
