Mersenne Prime
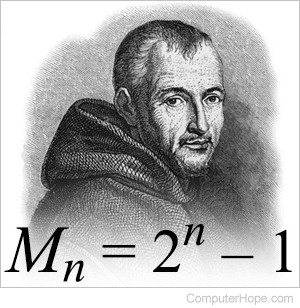
A Mersenne prime is any prime number that is a power of 2, minus 1. It is defined as Mn = 2n - 1, where n is any integer.
For instance, the prime number 3 is a Mersenne prime, because it equals 22 - 1. The next seven Mersenne primes are 7 (n=3), 31 (n=5), 127 (n=7), 8191 (n=13), 131071 (n=17), 524287 (n=19), and 2147483647 (n=31). As the sequence continues, the numbers get large very quickly.
Mersenne primes are named after Marin Mersenne, a French friar and polymath who studied them in the 17th century. Among other important functions, Mersenne primes are used in the Mersenne Twister, a widely-used PRNG (pseudorandom number generator) algorithm.
GIMPS

Today, Mersenne primes are calculated by volunteer computing users all over the world, as part of GIMPS (Great Internet Mersenne Prime Search). Since November 13, 1996, all new Mersenne primes have been discovered by GIMPS users who volunteer the unused cycles on their home computers.
The largest known Mersenne prime was discovered on December 7, 2018, by GIMPS user Patrick Laroche in Ocala, Florida, using an i5-4590T CPU (central processing unit) operating at 2.0 GHz. The number, 282589933-1, has 24,862,048 digits. It is the 51st Mersenne prime to be discovered. It is not necessarily the next prime in the sequence, however, because numerically smaller candidates are still being tested by other GIMPS users.
