Tree topology
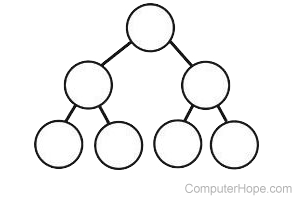
A tree topology is a special type of structure where many connected elements are arranged like the branches of a tree. For example, tree topologies are frequently used to organize the computers in a corporate network, or the information in a database.
In a tree topology, there can be only one connection between any two connected nodes. Because any two nodes can have only one mutual connection, tree topologies create a natural parent and child hierarchy.
Tree topology in computer networking
In computer networks, a tree topology is also known as a star bus topology. It incorporates elements of both a bus topology and a star topology. Below is an example network diagram of a tree topology, where the central nodes of two star networks are connected to one another.
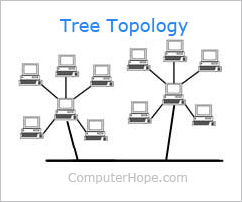
In the picture, if the main cable (trunk) between the two star topology networks failed, those networks would be unable to communicate with each other. However, computers on the same star topology would still be able to communicate.
Tree topology in computer programming
In computer programming, tree topologies can structure many kinds of data, including a computer program itself.
For example, this is a computer program written in Lisp:
(+ 1 2 (if (> p 10) 3 4))
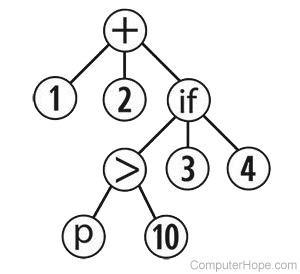
This program says "If p is greater than 10, add the numbers 1, 2, and 3. Otherwise, add the numbers 1, 2, and 4." Like all Lisp programs, it has an inherent tree topology structure. If we draw it as a graph, it looks like the tree shown at right. Representing a program this way can be useful because it clearly shows how all the operations and data are connected.
Programs in this kind of structure also have special uses. For instance, genetic programming techniques can evolve new computer programs by exchanging branches between existing programs structured as trees.
Tree topology in binary trees
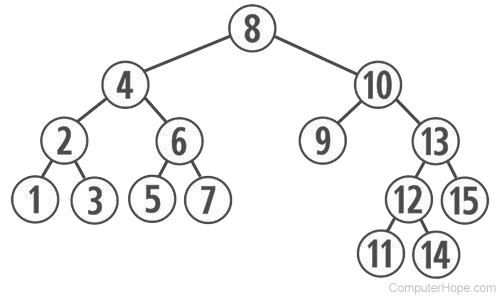
A binary tree is a tree topology where every node has a maximum of two children. The child nodes are labeled as "left child" or "right child." This type of data structure is used for sorting and searching large amounts of data. In the binary tree shown below, each parent's left child has a value less than the right child.
B-trees
A B-tree is a variation of a binary tree that was invented by Rudolf Bayer and Ed McCreight at Boeing Labs in 1971. Its nodes have children that fall within a predefined minimum and maximum, usually between 2 and 7. A B-tree graph might look like the image below.
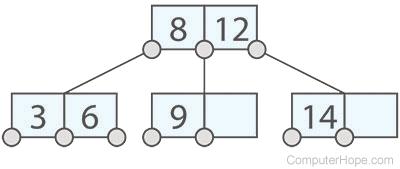
B-trees are "self-balancing," meaning the height of the branches is managed so that they do not get arbitrarily large. Each node contains partitioning "key values" that indicate the values of the children. Their design is optimized for handling large data files, and for writing data to memory or disk. They are used extensively in database systems like MySQL, PostgreSQL, and Redis, and filesystems such as NTFS (NTFS file system), HFS+, and ext4.
