Diffie-Hellman key exchange

The Diffie-Hellman key exchange was the first Public Key Cryptography developed by Whitfield Diffie and Martin Hellman in 1976. It's a key exchange algorithm that allows two parties to generate a shared secret key over an insecure communication channel. Essentially, the contents of any secret are safe as long as the private keys remain anonymous.
It was a groundbreaking concept for encryption because even if an eavesdropper intercepts the public keys, they can't easily derive the secret without knowing the private ones. Its difficulty is due to the discrete logarithm problem protecting the private keys, which is CPU (Central Processing Unit) resource-intensive to solve.
The process for setting up and using a Diffie-Hellman key exchange starts with both parties agreeing on two numbers: a large prime and a primitive root modulo. Then, each party chooses a secret private key. Using the agreed-upon prime number and primitive root, each party computes a public key and shares it with the other. Each party combines their private key with the other party's public key to compute the shared secret key.
Simplified explanation of a Diffie-Hellman key exchange
To simplify this explanation, we use two individuals, Sherry and Carl, and paint colors instead of numbers.
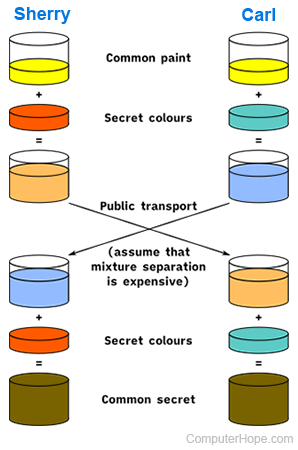
To begin, Sherry and Carl openly choose an initial color of yellow. Simultaneously, each person privately chooses a personal color: red for Sherry and cyan for Carl. The key step involves Sherry and Carl blending their secret colors with the jointly agreed-upon color, resulting in orange-tan and light blue combinations, respectively. Then, they openly swap these mixed colors. Finally, each blends the color received from their partner with a private color, yielding a color amalgamation (yellow-brown in this instance) mirroring their partner's final color blend.
If the secret were intercepted, only the common color (yellow) and the first mixtures (orange-tan and light blue) are known, but the secret colors would be difficult to know.
Coming full circle to a real-life exchange using numbers rather than paint colors, this determination is computationally expensive (requires a lot of calculating power). Essentially, it's impossible to compute the private number in a reasonable time, even for today's supercomputers.
There's some concern that future quantum computers could calculate so fast that it would break this encryption. However, until that time comes, this encryption remains safe because of how long it takes to decrypt.
Asymmetric encryption, Encryption, Key, Man-in-the-middle attack, Mirroring, Prime number, Security terms
